Neighborhood Operators
This module provides various neighborhood structures for cellular genetic algorithms (CGAs). Neighborhood structures define how individuals interact with others in their immediate vicinity, playing a critical role in regulating the flow of information and maintaining diversity within the population.
In cellular genetic algorithms, the concept of neighborhoods is integral to the evolutionary process. As shown in the diagram below, each individual in the population interacts with its neighbors during key stages of the evolutionary cycle: Selection, Recombination, Mutation, and Replacement. This localized interaction helps balance exploration and exploitation, promoting better local optimization while preserving diversity.
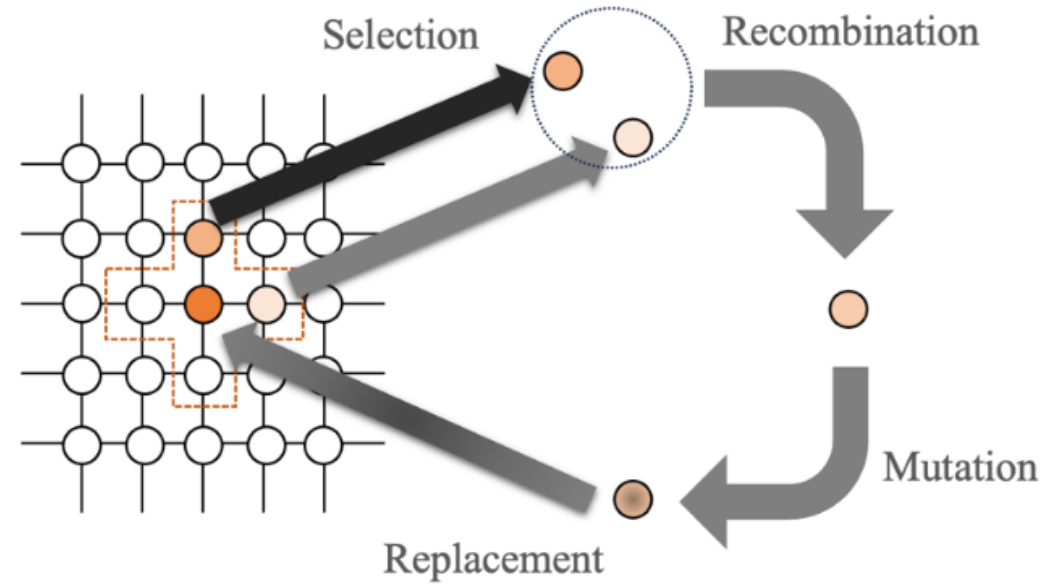
Figure 1: A representation of the reproduction cycle with neighborhood structure in a cellular genetic algorithm.
The neighborhood structure governs which individuals are selected for interactions during the evolutionary cycle. Depending on the problem requirements, users can choose different types of neighborhoods, such as linear or compact structures, to optimize the algorithm’s performance.
The Concept of Neighborhood
Neighborhood refers to a spatial structure used to improve solutions in optimization problems. In most cases, the neighborhood of a solution represents solutions obtained through small modifications.
Below are some popular neighborhood structures:
Linear Neighborhood: Individuals interact with neighbors arranged in a straight line.
Compact Neighborhood: A structure formed by cells surrounding an individual, allowing denser interaction.
Why Use Different Structures?
Each neighborhood structure is suited for specific problem types: - Linear structures are more appropriate for sequential or ordered problems. - Compact structures are ideal for scenarios requiring dense information sharing and local exploration.
Neighborhood Scheme Examples
Linear Neighborhood A linear neighborhood structure refers to an arrangement where individuals interact with a specific number of neighbors in a straight line. For instance, consider a linear structure with 5 neighbors:
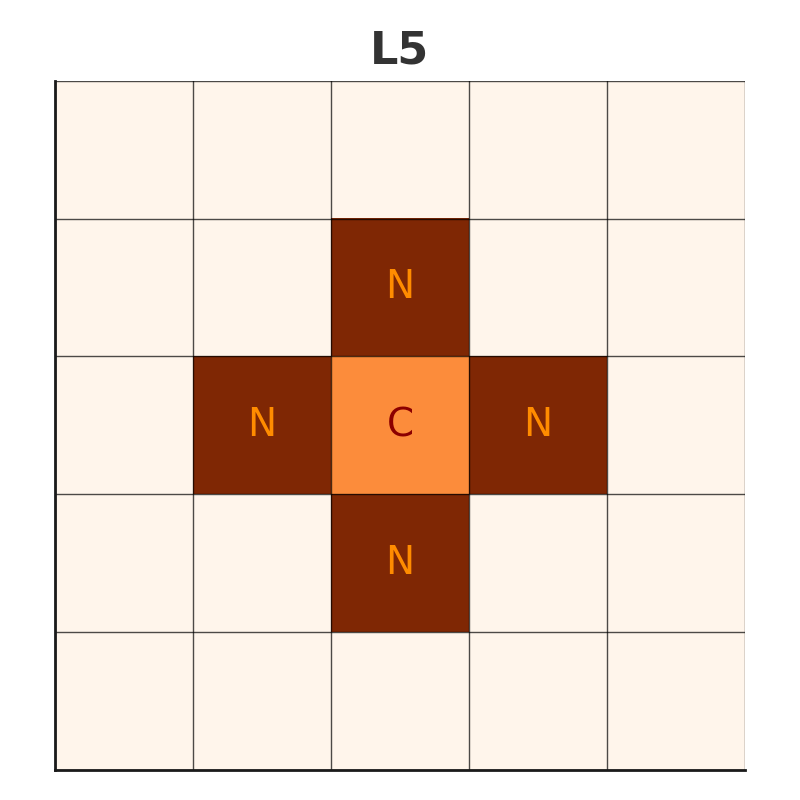
Figure 2: Linear 5 Neighborhood Structure
Each individual shares information only with its immediate neighbors. This structure is suitable for cases requiring limited information flow.
Compact Neighborhood Compact structures involve individuals sharing information intensively with all their surrounding neighbors. Below is an example of a compact structure with 9 neighbors:
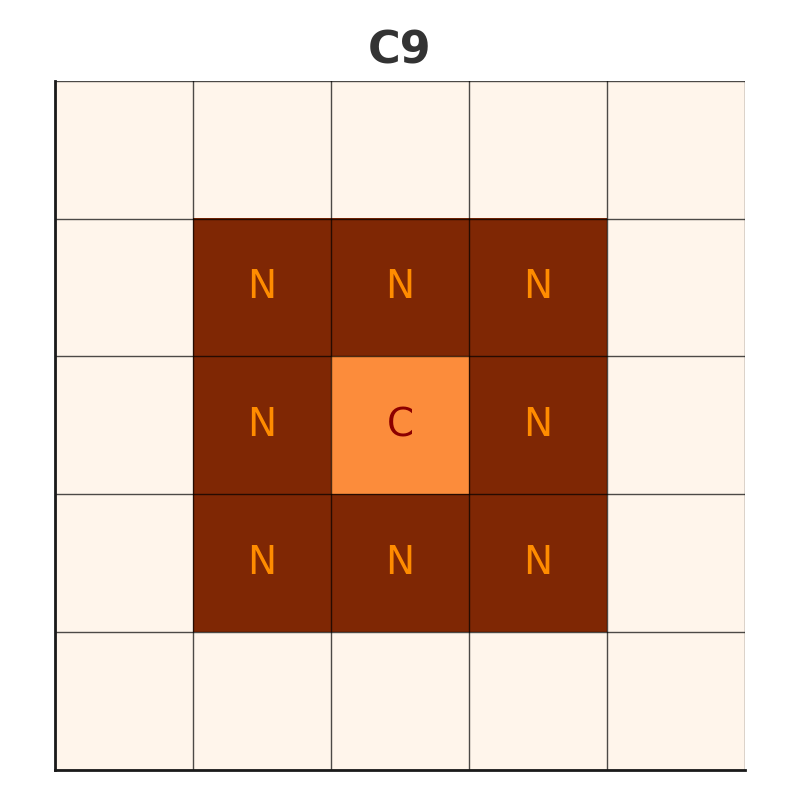
Figure 3: Compact 9 Neighborhood Structure
This structure can achieve faster convergence but must be used cautiously to maintain diversity.
API References
The following sections provide detailed documentation for the neighborhood operators available in the pycellga.neighborhoods package.
Linear 5
Description: A structure with 5 neighbors in a linear arrangement.
- class Linear5(position, n_rows, n_cols)[source]
Bases:
objectLinear5 calculates the positions of the 4 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.
Linear 9
Description: A linear arrangement with 9 neighbors for greater information flow.
- class Linear9(position, n_rows, n_cols)[source]
Bases:
objectLinear9 calculates the positions of the 8 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.
Compact 9
Description: A compact structure with 9 neighbors for dense interaction.
- class Compact9(position, n_rows, n_cols)[source]
Bases:
objectCompact9 calculates the positions of the 8 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.
Compact 13
Description: A compact structure with 13 neighbors.
- class Compact13(position, n_rows, n_cols)[source]
Bases:
objectCompact13 calculates the positions of the 12 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.
Compact 21
Description: A compact structure with 21 neighbors for broader information sharing.
- class Compact21(position, n_rows, n_cols)[source]
Bases:
objectCompact21 calculates the positions of the 20 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.
Compact 25
Description: An extended compact structure with 25 neighbors for enhanced information sharing.
- class Compact25(position, n_rows, n_cols)[source]
Bases:
objectCompact25 calculates the positions of the 24 neighbors in a 2D grid for a given position, considering wrapping at the grid edges.
- Parameters:
position (tuple) – The (x, y) position of the point whose neighbors are to be calculated.
n_rows (int) – The number of rows in the grid.
n_cols (int) – The number of columns in the grid.